Question 8.39

Let \(S\) be the portion of the plane \(2x + 3y + z = 5\) lying between the points \((-1,1,4)\), \((2,1,-2)\), \((2,3,-8)\), and \((-1,3,2)\). Find parameterizations for both the surface \(S\) and its boundary \(\partial\! S\). Be sure that their respective orientations are compatible with Stokes’ theorem.

Question 8.40

Let \(S\) be the portion of the surface \(z = x^2 + y^2\) lying between the points \((0,0,0)\), \((2,0,4)\), \((0,2,4)\), and \((2,2,8)\). Find parameterizations for both the surface \(S\) and its boundary \(\partial\! S\). Be sure that their respective orientations are compatible with Stokes’ theorem.

Question 8.41

\begin{eqnarray*} S & = & \{ (x,y,z) : x^2 + y^2 + z^2 = 1, \quad z \geq 0 \} \\[4pt] &&\quad \hbox{(oriented as a graph)}\\[4pt] \partial\! S & = & \{ (x,y) : x^2 + y^2 = 1 \} \\ \textbf{F} & = & x \textbf{i} + y \textbf{j} + z \textbf{k}\\[-19pt] \end{eqnarray*}

Question 8.42

\(S\) as in (1), and \(\textbf{F} = y \textbf{i} + z \textbf{j} + x \textbf{k}\)

Question 8.43

\begin{eqnarray*} S & = & \{ (x,y,z) : z = 1- x^2 - y^2, \quad z \geq 0 \} \\[4pt] &&\quad \hbox{(oriented as a graph)}\\[4pt] \partial\! S & = & \{ (x,y) : x^2 + y^2 = 1 \} \\ \textbf{F} & = & z \textbf{i} + x \textbf{j} + (2zx + 2xy) \textbf{k} \end{eqnarray*}

Question 8.44

\(S\) as in (3), and \(\textbf{F} = z^2 \textbf{i} + x \textbf{j} + y^2 \textbf{k}\)

Question 8.45

Let \(C\) be the closed, piecewise smooth curve formed by traveling in straight lines between the points \((0,0,0)\), \((2,0,4)\), \((3,2,6)\), \((1,2,2)\), and back to the origin, in that order. (Thus the surface \(S\) lying interior to \(C\) is contained in the plane \(z=2x\).) Use Stokes’ theorem to evaluate the integral: \[ \int_{C} (z \cos x)\, {\it dx} + (x^2 y z)\, {\it dy} + (yz)\, dz \]

451

Question 8.46

Let \(C\) be the closed, piecewise smooth curve formed by traveling in straight lines between the points \((0,0,0)\), \((2,1,5)\), \((1,1,3)\), and back to the origin, in that order. Use Stokes’ theorem to evaluate the integral: \[ \int_{C} (xyz)\,{\it dx} + (x y)\,{\it dy} + (x)\,dz \]

Question 8.47

Redo Exercise 9 of Section 7.6 using Stokes’ theorem.

Question 8.48

Redo Exercise 10 of Section 7.6 using Stokes’ theorem.

Question 8.49

Verify Stokes’ theorem for the upper hemisphere \(z= \sqrt{1-x^2- y^2}, z \ge 0\), and the radial vector field \({\bf F} (x,y,z)= x {\bf i} + y {\bf j} +z {\bf k}\).

Question 8.50

Let \(S\) be a surface with boundary \(\partial\! S\), and suppose \({\bf E}\) is an electric field that is perpendicular to \(\partial\! S\). Show that the induced magnetic flux across \(S\) is constant in time. (HINT: Use Faraday’s law.)

Question 8.51

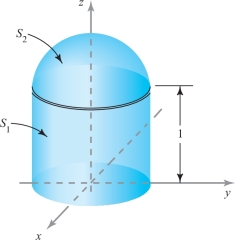
Let \(S\) be the capped cylindrical surface shown in Figure 8.23. \(S\) is the union of two surfaces, \(S_1\) and \(S_2\), where \(S_1\) is the set of \((x,y,z)\) with \(x^2 + y^2=1, 0 \le z \le 1\), and \(S_2\) is the set of \((x,y,z)\) with \(x^2 + y^2 + (z-1)^2 =1, z \ge 1\). Set \({\bf F} (x,y,z) = (zx + z^2 y + x) {\bf i} + ( z^3 yx + y) {\bf j}+ z^4 x^2 {\bf k}\). Compute \({\intop\!\!\!\intop}_S ( {\nabla}\times {\bf F}) \,{\cdot}\, d {\bf S}\). (HINT: Stokes’ theorem holds for this surface.)

Question 8.52

Let \({\bf c}\) consist of straight lines joining \((1, 0, 0), (0, 1, 0)\), and \((0, 0, 1)\) and let \(S\) be the triangle with these vertices. Verify Stokes’ theorem directly with \({\bf F} = yz {\bf i} + xz {\bf j}+ xy {\bf k}\).

Question 8.53

Evaluate the integral \({\intop\!\!\!\intop}_S ({\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S}\), where \(S\) is the portion of the surface of a sphere defined by \(x^2 + y^2 + z^2=1\) and \(x+ y +z \ge 1\), and where \({\bf F}= {\bf r} \times ({\bf i} + {\bf j} + {\bf k}), {\bf r}= x {\bf i}+ y {\bf j} + z {\bf k}\).

Question 8.54

Show that the calculation in Exercise 15 can be simplified by observing that \(\int_{\partial\! S} {\bf F}\,{\cdot}\, d{\bf r}=\int_{\partial\!\Sigma}{\bf F}\,{\cdot}\, d{\bf r}\) for any other surface \(\Sigma\). By picking \(\Sigma\) appropriately, \({\intop\!\!\!\intop}_{\Sigma} ({\nabla} \times {\bf F}) \,{\cdot}{\,d} {\bf S}\) may be easy to compute. Show that this is the case if \(\Sigma\) is taken to be the portion of the plane \(x+ y + z=1\) inside the circle \(\partial\! S\).

Question 8.55

Calculate the surface integral \({\intop\!\!\!\intop}_S ({\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S}\), where \(S\) is the hemisphere \(x^2 {+} y^2 {+} z^2 = 1, x \ge 0\), and \({\bf F}= x^3 {\bf i} - y^3 {\bf j}\).

Question 8.56

Find \({\intop\!\!\!\intop}_S ({\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S}\), where \(S\) is the ellipsoid \(x^2 + y^2 + 2 z^2 =10\) and \({\bf F}\) is the vector field \({\bf F} = (\sin xy) {\bf i} + e^x {\bf j} - yz {\bf k}\).

Question 8.57

Let \({\bf F} = y {\bf i} \,-\, x {\bf j} \,+\, z x^3 y^2 {\bf k}\). Evaluate \({\intop\!\!\!\intop}_S ({\nabla} \times {\bf F}) \,{\cdot}\, {\bf n} {\,d} A\), where \(S\) is the surface defined by \(x^2 \,+\, y^2 \,+\, z^2 =1, z \le 0\).

Question 8.58

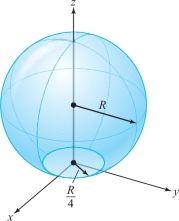
A hot-air balloon has the truncated spherical shape shown in Figure 8.24. The hot gases escape through the porous envelope with a velocity vector field \begin{eqnarray*} &&{\bf V} (x,y,z) = {\nabla} \times {\Phi} (x,y,z)\\ &&\qquad\hbox{where}\qquad {\Phi} (x,y,z) = -y {\bf i}+ x {\bf j}. \end{eqnarray*}

If \(R=5\), compute the volume flow rate of the gases through the surface.

Question 8.59

Prove that Faraday’s law implies \({\nabla} \times {\bf E}= -\partial {\bf H} / \partial t\).

Question 8.60

Let \(S\) be a surface and let \({\bf F}\) be perpendicular to the tangent to the boundary of \(S\). Show that \[ \intop\!\!\!\intop\nolimits_{S} ({\nabla} \times {\bf F}) \,{\cdot}\, d {\bf S} =0. \]

What does this mean physically if \({\bf F}\) is an electric field?

452

Question 8.61

Consider two surfaces \(S_1, S_2\) with the same boundary \(\partial\! S\). Describe with sketches how \(S_1\) and \(S_2\) must be oriented to ensure that \[ \intop\!\!\!\intop\nolimits_{S_1} ({\nabla} \times {\bf F})\,{\cdot}\, {\,d} {\bf S} = \intop\!\!\!\intop\nolimits_{S_2} ({\nabla} \times {\bf F})\,{\cdot}\, d {\bf S}. \]

Question 8.62

For a surface \(S\) and a fixed vector \({\bf v}\), prove that \[ 2 \intop\!\!\!\intop\nolimits_{S} {\bf v} \,{\cdot}\, {\bf n}\, dS = \int_{\partial\! S} ({\bf v} \times {\bf r})\,{\cdot}\, d {\bf s}, \] where \({\bf r} (x,y,z) = (x,y,z)\).

Question 8.63

Argue informally that if \(S\) is a closed surface, then \[ \intop\!\!\!\intop\nolimits_{S} ({\nabla} \times {\bf F})\,{\cdot}\,d {\bf S} =0 \] (see Exercise 23). (A closed surface is one that forms the boundary of a region in space; thus, for example, a sphere is a closed surface.)

Question 8.64

If \(C\) is a closed curve that is the boundary of a surface \(S\), and \(f\) and \(g\) are \(C^2\) functions, show that

• (a) \(\displaystyle\int_C f {\nabla}\! g \,{\cdot}\, d {\bf s} = {\intop\!\!\!\intop}_S ({\nabla}\! f \times {\nabla} g) \,{\cdot}\, d {\bf S}\)
• (b) \(\displaystyle\int_C (f {\nabla}g + g {\nabla}f) \,{\cdot}\, d {\bf s} = 0\)

Question 8.65

• (a) If \(C\) is a closed curve that is the boundary of a surface \(S\), and \({\bf v}\) is a constant vector, show that \[ \int_C {\bf v} \,{\cdot}\,d {\bf s} =0. \]
• (b) Show that this is true even if \(C\) is not the boundary of a surface \(S\).

Question 8.66

Show that \({\Phi}\colon\, D \to {\mathbb R}^3, D = [0, \pi] \times [0, 2 \pi], {\Phi} (\phi, \theta) = (\cos \theta \sin \phi\), \(\sin \theta \sin \phi\), \(\cos \phi)\), which parametrizes the unit sphere, takes the boundary of \(D\) to half of a great circle on \(S\).

Question 8.67

Verify Theorem 6 for the helicoid \({\Phi} (r, \theta)= (r \cos \theta, r \sin \theta, \theta) , (r, \theta) \in [0,1] \times [0, \pi/2]\), and the vector field \({\bf F} (x,y,z) = (z,x,y)\).

Question 8.68

Prove Theorem 6.

Question 8.69

Let \({\bf F} = x^2 {\bf i}+ (2xy + x) {\bf j} +z {\bf k}\). Let \(C\) be the circle \(x^2 + y^2 =1\) and \(S\) the disc \(x^2 + y^2 \le 1\) within the plane \(z=0\).

• (a) Determine the flux of \({\bf F}\) out of \(S\).
• (b) Determine the circulation of \({\bf F}\) around \(C\).
• (c) Find the flux of \({\nabla} \times {\bf F}\). Verify Stokes’ theorem directly in this case.

Question 8.70

Let \(S\) be a surface with boundary \(\partial\! S\), and suppose that \(\bf E\) is an electric field that is perpendicular to \(\partial\! S\). Use Faraday’s law to show that the induced magnetic flux across \(S\) is constant in time.

Question 8.71

Integrate \({\nabla} \times {\bf F, F}= (3y, -xz, -yz^2)\) over the portion of the surface \(2z = x^2 + y^2\) below the plane \(z=2\), both directly and by using Stokes’ theorem.

Question 8.72

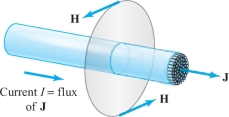
Ampère’s law states that if the electric current density is described by a vector field \({\bf J}\) and the induced magnetic field is \({\bf H}\), then the circulation of \({\bf H}\) around the boundary \(C\) of a surface \(S\) equals the integral of \({\bf J}\) over \(S\) (i.e., the total current crossing \(S\)). See Figure 8.25. Show that this is implied by the steady-state Maxwell equation \({\nabla} \times {\bf H} ={\bf J}\).

Question 8.73

Faraday’s law relates the line integral of the electric field around a loop \(C\) to the surface integral of the rate of change of the magnetic field over a surface \(S\) with boundary \(C\). Regarding the equation \({\nabla} \times {\bf E} = - \partial {\bf H} / \partial t\) as the basic equation, Faraday’s law is a consequence of Stokes’ theorem, as we have seen in Example 4.

Suppose we are given electric and magnetic fields in space that satisfy \({\nabla} \times {\bf E}= - \partial {\bf H} / \partial t\). Suppose \(C\) is the boundary of the Möbius band shown in Figures 7.6.3 and 7.6.4. Because the Möbius band cannot be oriented, Stokes’ theorem does not apply. What becomes of Faraday’s law? What do you guess \(\int_C {\bf E} \,{\cdot}\, d {\bf s}\) equals?

Question 8.74

• (a) If in spherical coordinates, we write \[ {\bf e}_r=\alpha {\bf i}+\beta{\bf j}+\gamma {\bf k}, \hbox{find}\ \alpha,\beta, \hbox{and}\ \gamma. \]
• (b) Find similar formulas for \({\bf e}_\phi\) and \({\bf e}_\theta\).